Recursive steate estimation

13 Jul 2017

The most essential problem in probabilistic robotics is to estimate the current state of robots from sensor data, which is always noisy or not directly observable. State Estimation draws this problem and seeks to recover state variable from sensor data, so that the state belief can be quantified by computing the belief distribution over possible world states. Let’s begin with basic probability at first.

Robot Environment Interaction

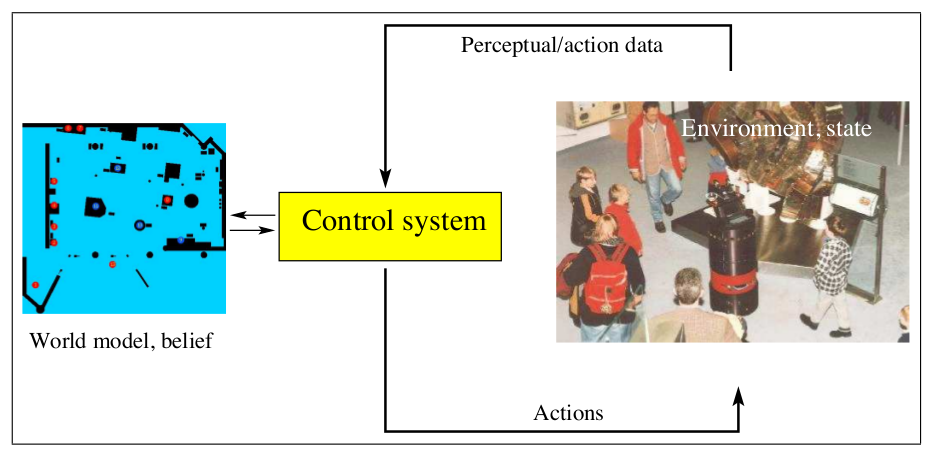
An environment or a world of robot is a dynamic system that possesses internal state. The robot percepts this world by its perception devices like sensor. However the sensor is noisy or the environment is not fully observable, so the robot maintains a internal belief state with regards to the state of its environment. An environment interaction is depicted as follows (Quote from Probabilistic Robotics):

A typical interaction environment in live world.

State

Environments can be abstracted as State. The state is call dynamic when it changes over time, say, the fuel lifetime of a robot. Static state means it’s changeless over time, e.g. the location of wall in a building. Also the state can be inferred to the robot itself, such as its pose, velocity and etc. State is often denoted as $x$, the state at time step $t$ is denoted as $x_t$. Typical state variables comprised from the following categories:

• The robot pose: it's the location and orientation relative to the global coordinate frame. Rigid mobile robots possess six such state variables, three for their Cartesian coordinates, and three for their angular orientation, also called Euler angles (pitch, roll, and yaw). The post state is ofter refereed to kinematic state.
• The configuration of Robot's Actuators: , such as the joints of robotic manipulators. Each degree of freedom in a robot arm is characterized by a one-dimensional configuration at any point in time, which is part of the kinematic state of the robot.
• The robot velocity and the velocities of its joints. A rigid robot moving through space is characterized by up to six velocity variables, one for each pose variables. Velocities are commonly referred to as dynamic state.
• The location and features of surrounding objects in the environment. How an object will be represented depending on the granularity of the state that is being modeled, robot environments possess between a few dozen and up to hundreds of billions of state variables. Sometime we use landmarks that are stationary and easily recognize reliably.
• The location and velocities of moving objects and people. Those objects have also the kinematic state.
• There can be a huge number of other state variables. For example, whether or not a sensor is broken is a state variable, as is the level of battery charge for a battery-powered robot.

A state $x_t$ is called complete if it’s the best predictor to the future. Completeness includes knowledges of states, measurements, or controls carry on no additional information that would help us to predict the future more accurately. Completeness does not imply that the future is a deterministic function of state. Completeness provides a good view theoretically and analytically. In practice it’s impossible to specify the robot to a complete state, which limited by different factors such as robot memory, or changing dynamic of environment and etc. Such a state is incomplete state. State spaces varies also different. Continuous state space like the robot pose, and discrete state space like battery is empty or not. Some is a mixture of both, called hybrid state space.

Interaction

As the carton above shows, an interaction between robot and its environment consists of two aspects:

• Sensor measurement: Perceptions enables the robots to percepts and gather information from the environment to determine its state in environment, e.g. using camera taking photos or scan range and etc. This perceptual information is called measurement or sometimes denoted as observation. Often the measurement arrives with some delay.
• Control actions: by which the world changes. The robot may execute a action or moves a little bit. Even the robot stays unmoved, the state changes unstop. In practice, the robot continuously executes controls and measurements are made concurrently.

All the collection of measurement and controls is denoted as data. The robot has normally two types of data in accordance with the interactions.
Measurement data: provides the momentary information about the state of environment. The measurement data at time $t$ is denoted as $z_t.$ Usually the robot can acquire variables numbers of measurement within a single time step. The measurements between time step $t_1$ and $t_2$ are denoted as \begin{equation} z_{t_1:t_2} = z_{t_1},z_{t_1 + 1}, z_{t_1 + 2}, \dots, z_{t_2} \end{equation}

Control data: presents the information about the change of state in environment. e.g. the motion of robot in environment. An alternative source of control data are obometers, which measures the revolution of robot’s wheels. Control data is denoted as $u_t$ at time step $t$. The control variable $u_t$ corresponds to the change of state in time interval $[ t-1,t ]$. A sequence of control data for $t_1 < t_2$ is denoted as:

\begin{equation} u_{t_1:t_2} = u_{t_1}, u_{t_1 +1}, u_{t_1 + 2}, \dots, u_{t_2} \end{equation}
As we saied before, even the robot does not execute actions, the state changes. Hence, we assume that there is exactly one control data item per time step $t$.

Probabilistic Generative Laws

The evolution of states and measurements is governed by the probabilistic laws. The state $x_t$ is generated stochastically. So it’s necessary to specify the probabilistic distribution from which the state $x_t$ is generated. Normally the current state $x_t$ is conditional on all past states, measurements and control, as denoted as follows: \begin{equation} p(x_t|x_{0:t-1}, z_{1:t-1}, u_{1:t}) \tag{1} \end{equation}

If the state is complete, it carries sufficient information about all what pasts in previous time steps. In particular, $x_{t-1}$ is a sufficient information about all previous states $u_{1:t_1}$ and measurements $z_{1:t-1}$ upto this point. So what matters is $u_t$ if we know the state $x_{t-1}$. Hence the Eq. (1) can be reformed as: \begin{equation}\label{eq:problaws2} p(x_t|x_{0:t-1}, z_{1:t-1}, u_{1:t}) = p(x_t|x_{t-1}, u_t) \tag{2} \end{equation} The Eq. (2) possess the conditional independence. Similar, the model of generating measurements also shows the conditional independence property as follows: \begin{equation}\label{eq:problaws3} p(z_t|x_{0:t},z_{1:t-1}, u_{1:t}) = p(z_t|x_t) \tag{3} \end{equation} This Eq. (3) shows that the current state $x_t$ is sufficient to predict the measurement $z_t$.

The Eq. (2) specifies how the environmental state changes over time as a function of control $u_t$, is called State Transition Probability. The stochastic dynamics of environment is clearly expressed by this quantity. Sometime the this transition distribution does not depend on the time index $t$, so this quantity may be denoted as \begin{equation} p(x^\prime|x, u), \end{equation} where $x$ the predecessor state and $x^\prime$ successor state.

The quantity (3) shows the probability with which the measurement is made, is called Measurement Prabability. If it does not involve time index, this can be reformed as \begin{equation} p(z|x). \end{equation}

Belief Distributions

A belief reflects the internal knowledge of robots about the state of the environment. The state can not be measured directly. Hence, we need to infer it from data. Therefore we distinguish the true state from its internal belief state or state of knowledge with regard to the state.

Belief distribution are posterior probability over state variables conditioned on the available data. The posterior belief distribution over state $x_t$ is given by: \begin{equation} bel{(x_t)} = p(x_t|z_{1:t}, u_{1:t}) \end{equation} Literally it says the state of knowledge of $x_t$ is conditional on all the previous measurements and controls. If we calculate the posterior before incorporating $z_t$, such a posterior will be denoted as follows: \begin{equation}\label{eq:beliefprediction} \tilde{bel}{(x_t)} = p(x_t|z_{1:t-1}, u_{1:t}) \tag{4} \end{equation} This is a prediction of current state belief in probabilistic filtering based on the previous state posterior, before incorporating at time $t$. Computing $bel(x_t)$ from $\tilde{bel(x_t)}$ is called correction or measurement update.

Bayes Filter

Usually the state is not directly observable, in practice the belief is calculated by Bayes Filter from measurement and control data. The pseudo-code of this algorithm is depicted as follows:

This algorithm is a recursive approach and it consists of two essential steps: In line 2, it involves the computing the belief state over state $x_t$ based on the prior belief over state $x_{t-1}$ and the control at time step $t$. This prediction over state $x_t$ is obtained by the integral (sum) of prior belief to $x_{t-1}$ and the probability $u_t$ that induces a transition from $x_{t-1}$ to $x_t$, as we named in Eq. (4). The second step is called measurement update which arises a multiplication of prediction $\tilde{del}(x_t)$ by the probability by which the measurement might be observed. As it states here, the result should be normalized, since the multiplication results are not probability, that’s what $\eta$ does in line 3. To compute the posterior recursively, the initial belief $bel(x_0)$ at time $t = 0$ is needed. The initial belief should be either uniform distribution or some distribution with certainty.